
P–P plots are sometimes limited to comparisons between two samples, rather than comparison of a sample to a theoretical model distribution. Notably, it will pass through the point (1/2, 1/2) if and only if the two distributions have the same median. (need a graph for this paragraph)Īs the above example illustrates, if two distributions are separated in space, the P–P plot will give very little data – it is only useful for comparing probability distributions that have nearby or equal location. Example Īs an example, if the two distributions do not overlap, say F is below G, then the P–P plot will move from left to right along the bottom of the square – as z moves through the support of F, the cdf of F goes from 0 to 1, while the cdf of G stays at 0 – and then moves up the right side of the square – the cdf of F is now 1, as all points of F lie below all points of G, and now the cdf of G moves from 0 to 1 as z moves through the support of G. The degree of deviation makes it easy to visually identify how different the distributions are, but because of sampling error, even samples drawn from identical distributions will not appear identical. The comparison line is the 45° line from (0,0) to (1,1), and the distributions are equal if and only if the plot falls on this line. Thus for input z the output is the pair of numbers giving what percentage of f and what percentage of g fall at or below z. Given two probability distributions, with cdfs " F" and " G", it plots ( F ( z ), G ( z ) ) This behavior is similar to that of the more widely used Q–Q plot, with which it is often confused.Ī P–P plot plots two cumulative distribution functions (cdfs) against each other: It works by plotting the two cumulative distribution functions against each other if they are similar, the data will appear to be nearly a straight line. Simplilearn offers Minitab training course online with Statistics.In statistics, a P–P plot ( probability–probability plot or percent–percent plot or P value plot) is a probability plot for assessing how closely two data sets agree, or for assessing how closely a dataset fits a particular model. Read more: Process Capability Analysis: Minitab with Statistics To know more about Normality Test, you can explore Simplilearn’s Minitab with Statistics Training. 05, we can assume the “Before” data is normal. Here we can notice that since the P value is greater than. Once we click ok, Minitab generates the probability plot in a separate window. While there are multiple kinds of normality tests available, the Anderson Darling Test is the most reliable and commonly used test. Now we click on Anderson-Darling and then click on OK. Double click on before in the left hand side box to select it. In this example, let us test the Column which has before, data for normality.

Click on Normality Test then enter the variables on the respective columns. Go to Start menu and then move to Basic Statistics. Go to File Menu, click Open Project and then load the file including Cholesterol levels at fasting.
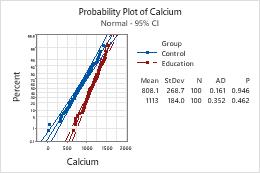
Example of conducting a Normality Test Taking the example of Cholesterol levels at fasting, before breakfast and after breakfast levels, let’s conduct a normality test. After clicking OK, Minitab generates the probability plot in a separate window. Step 3: Click on Normality Test and then enter the variables on the respective columns. Step 2: Go to Start menu and then move to Basic Statistics. Step 1: Go to File menu, click Open Project and then load the data to be analyzed. Let’s have a look at the steps to perform a normality test using Minitab.
Minitab has statistical tools that allow one to perform statistical calculations with ease. One can conduct a Normality test using Minitab. Many statistical analyses require that the data come from normally distributed populations. The normal distribution is the most common statistical distribution because approximate normality arises naturally in many physical, biological, and social measurement situations. A normal distribution is a bell-shaped curve that is symmetric about its mean. Normality Test helps one to determine whether a data is following a normal distribution or not. Normality is one of the major concepts in statistics used for various statistical calculations.


 0 kommentar(er)
0 kommentar(er)
